Aptitudes testées
Cet test permet une évalutation rapide de "l'intelligence générale fluide".
Cet test permet une évalutation rapide de "l'intelligence générale fluide".
Une suite ou matrice de dominos vous est donnée dans l'encadré. Un domino en rose est manquant, soit en partie, soit totalement. Vous devez trouver quel est ce domino en le sélectionnant dans la partie de réponse (partie avec "?")
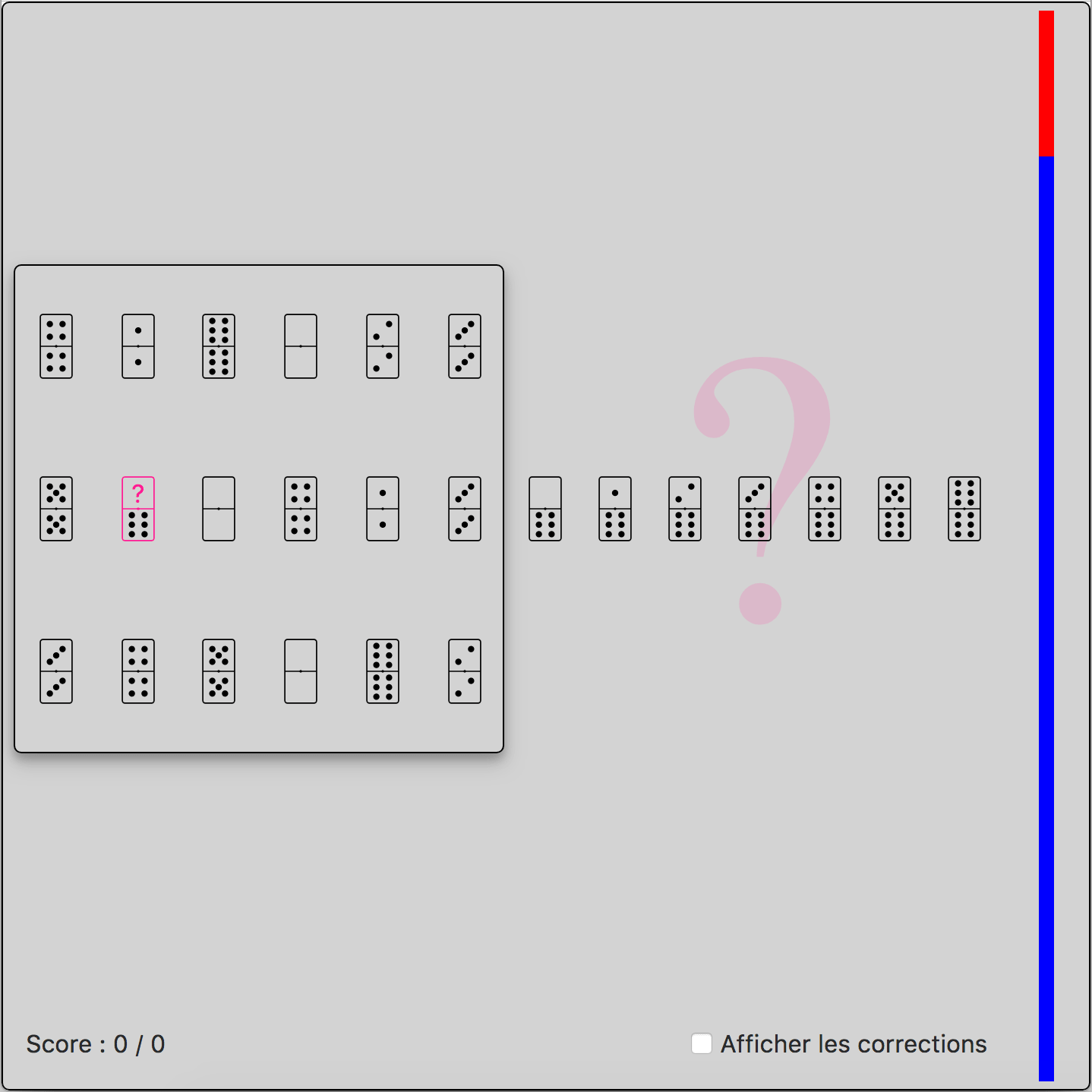
Dans l'exemple ci-contre, on voit que tous les dominos ont un écart nul entre le haut et le bas. La bonne réponse est donc le domino "(6/6)"
Vous devez effectuer 20 questions en 30 secondes chacune.
Important : lorsque vous additionnez ou soustrayez des quantités aux chiffres d'un domino, si vous dépassez 6, vous devez recommencer de 0. De même, si vous tombez en dessous de 0, vous devez repartir de 6.
Le tutoriel ci-dessous regroupe l'ensemble des logiques de notre test ainsi que des test D48/70 et 2000 originaux. Nous vous invitons à vous y habituer pour les détecter et les résoudre rapidement lorsque vous les rencontrez. Notez enfin que les exemples ci-dessous sont donnés indifféremment sur les lignes ou colonnes. Les mêmes logiques sont à retenir respectivement sur les colonnes et les lignes.