Aptitudes testées
On explore dans ce test la capacité du candidat à raisonner sur des données logiques simples et en tirer des conséquences.
On explore dans ce test la capacité du candidat à raisonner sur des données logiques simples et en tirer des conséquences.
Deux proposition sont énoncées. À partir des ces deux propositions, vous devez dire laquelle des quatre réponses en dessous est une conséquence logique des deux propositions initiales.
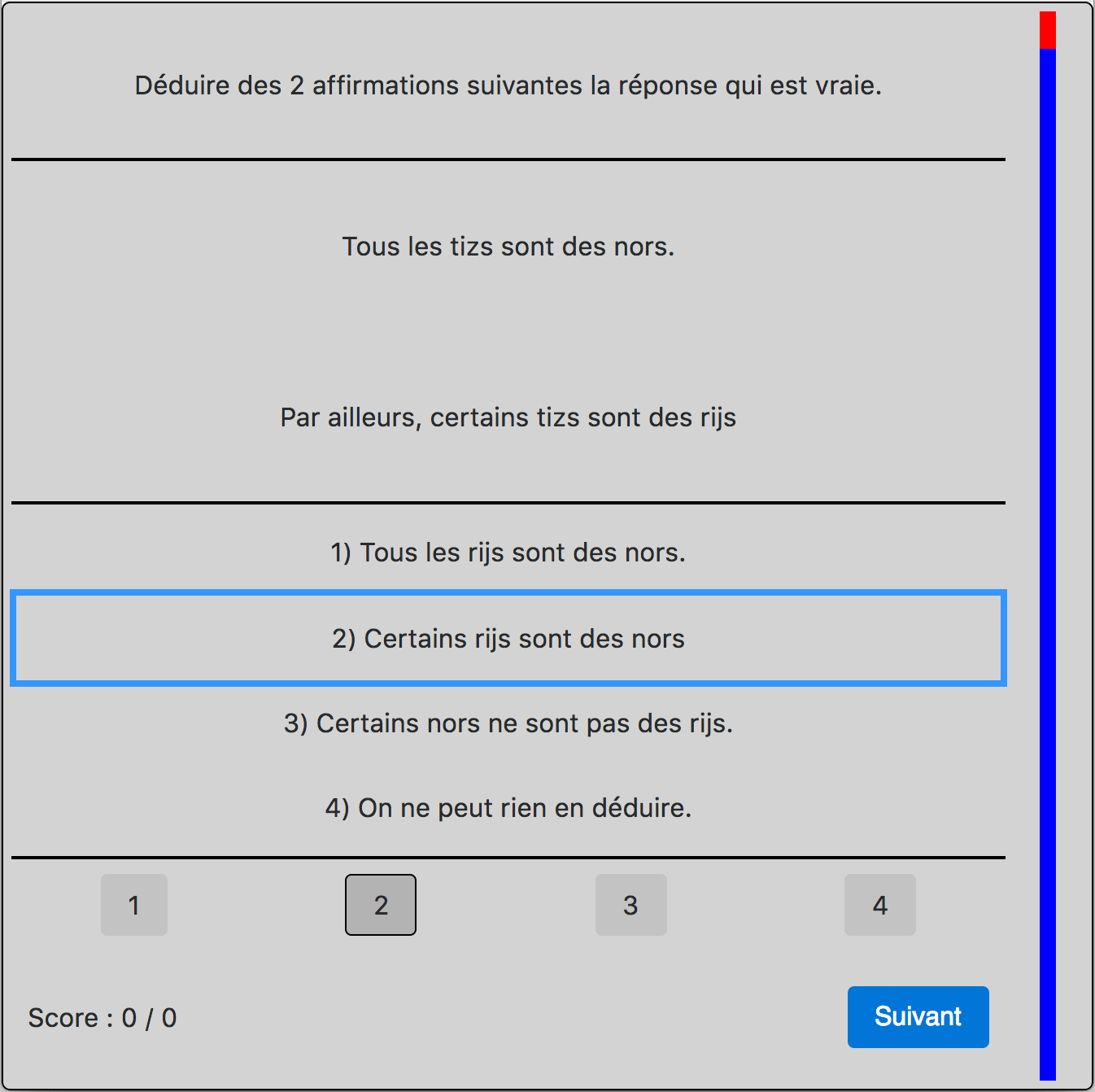
Si "Tous les tizs sont des nors" et si "Certains tizs sont des rijs" alors certains rijs (au moins ceux qui sont des tizs) sont des nors. Il est donc vrai de dire que "Certains rijs sont des nors." La bonne réponse est donc la 2)
Vous devez traiter 30 exercices en 10 minutes.
Suite à vos retours et questions, nous mettons en ligne quelques pistes de raisonnement pour ce test. Traduisons déjà mathématiquement et proprement ce que cachent les tournures employées dans cet exercice :